Cycling science

5 Mar 2025

Project introduction

The goal of this study was to use Computational Fluid Dynamics (CFD) simulations to analyze the aerodynamic differences between two road cycling postures; one featured a 175 mm crank length and the other utilized a shorter 165 mm crank length. The simulations were conducted using a model of a real cyclist (excluding the bicycle) riding at a speed of 14 m/s (50.4 km/h) with no lateral wind. The shorter crank length enabled the cyclist to lower his torso, assuming what is considered a more aerodynamic posture. The simulations confirmed this assumption and revealed that torso rotation is the most crucial parameter in reducing the frontal area and achieving a more streamlined airflow.

Laboratory setup

A representative cyclist (male, 24 years old, 1.76 m in height, 65 kg in weight) was selected from a group of eight high-level competitive road cyclists. These cyclists were previously analyzed for biomechanical changes associated with shorter crank use in our study, Changes in lower limb kinematics, kinetics, and muscle activity in cyclists using a shorter crank. . In the QEF laboratory, the selected cyclist was tested while riding with his standard longer cranks and shorter crank lenghts. Markers were placed on all relevant bony landmarks to accurately reproduce the kinematics of the lower limbs and the position of the upper body.
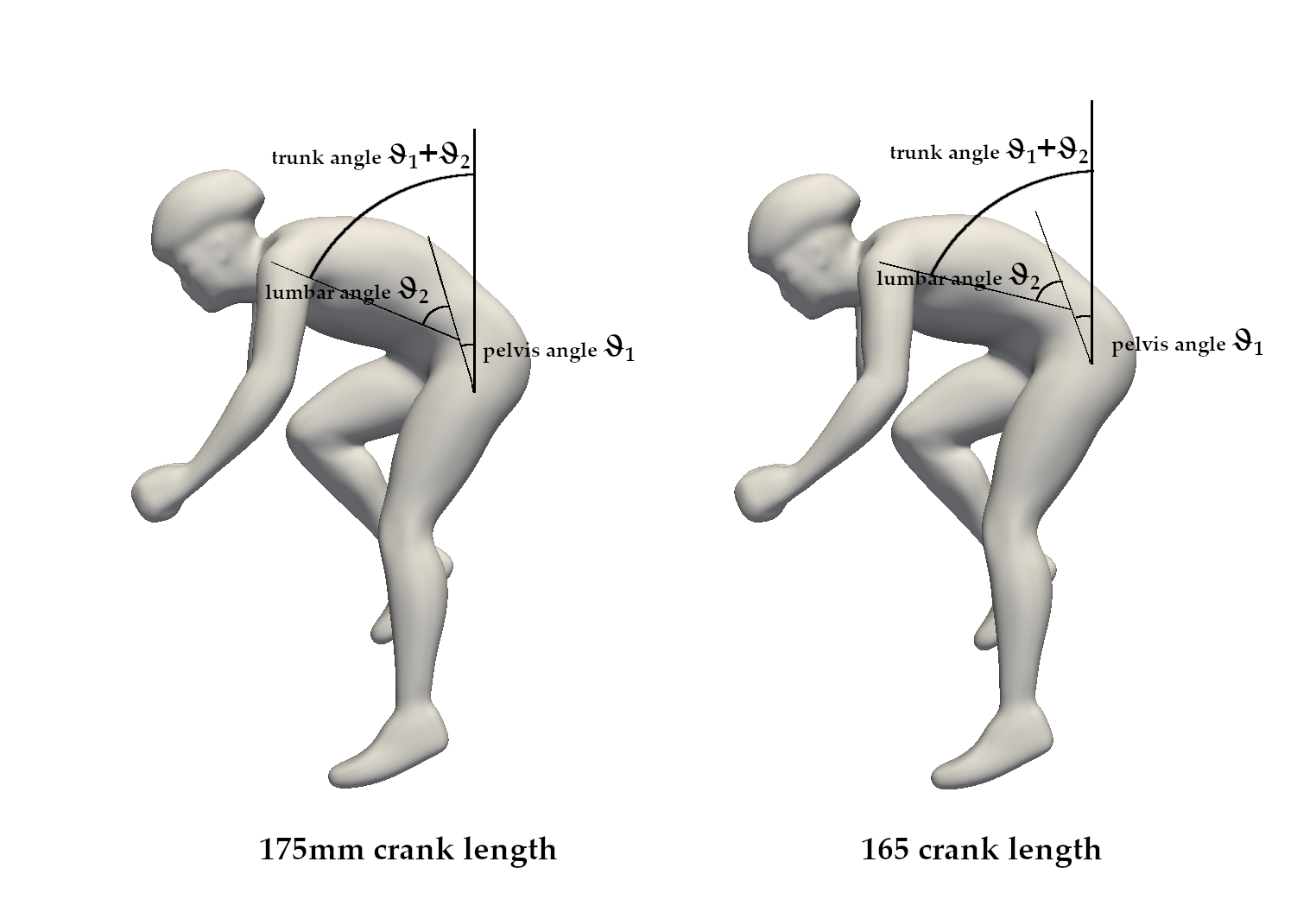
To maintain consistent leg angles at maximum extension (165º in the crank cycle, with 0º defined as the Top Dead Center - TDC), the cyclist adjusted the saddle upward and slightly backward, while keeping the same seatpost angle. The height and anterior/posterior position of the handlebars remained unchanged between the two testing conditions, and the cyclist was instructed to keep his hands on the hoods. Due to the shorter crank arm, the hip joint experienced less flexion when transitioning over the TDC, enabling a downward rotation of the torso, commonly referred to as a lower trunk posture. The cyclist exhibited an average trunk angle ϑ₁ +ϑ₂, relative to the vertical axis, of 68.9º in the first condition and 74.4º in the second (Figure 1). The leg position for the simulation was chosen, as depicted in Figure 1, to represent the most asymmetric case, as it could differentiate the left and right aerodynamic responses in the lower part of the body.

torso_inclination — Figure 1: Cyclist`s position with a 175 mm crank length and a 165 mm crank length - with the left leg at 165º in the crank cycle

3D-computer model

The cyclist’s body in a standing position was reproduced using a 3D scan. The resulting model was then used to precisely model the cyclist in Blender 3D, a computer graphics software. A mechanical skeleton rig was added to this final model. This process involves creating the necessary bones to move all body segments as desired. While this procedure is initially more time-consuming, it allows the body to be posed in more realistic cycling positions. In contrast, using a static 3D scan of the cyclist on his bicycle would result in lower limb angles that are not consistent with the loaded condition. Additionally, having a Blender file with an adaptive rig enables the exact replication of the cyclist’s movements when pedaling in different positions and/or at varying workload intensities with simple adjustments. Finally, Blender also allows for simplifying the model by omitting details that are insignificant or detrimental to the simulation.

3D model with rig — Figure 2: Rigged 3D cyclist. Image shows, as an example, the knee tool that allows it to rotate around 3 axes. The body has 52 tools to actuate the joints.

CFD simulation scheme

OpenFOAM, an open-source CFD code, was used for the simulations, assuming no crosswind and a cyclist speed of 14 m/s (50.4 km/h). An unsteady simulation with the k-ω SST turbulence model was initially employed, applying a turbulence intensity of 1%. To obtain an initial result, the potentialFoam solver was used, which assumes that the flow is incompressible, non-rotating, non-viscous, and has uniformly zero vorticity.
Subsequently, since the initial transient was not of interest, a steady simulation was conducted, starting with a first-order discretization scheme and later switching to a second-order scheme. As the final step, the PISO (Pressure-Implicit with Splitting of Operators) solver, a pressure-based algorithm designed for transient simulations of incompressible flows, was applied with a second-order discretization scheme. The time step was constrained to a maximum CFL (Courant-Friedrichs-Lewy) number of 0.9.
During the simulation, the minimum and maximum values of the field variables were monitored to ensure they did not oscillate or diverge to unrealistic values, and the continuity errors were checked to decrease. Convergence was verified through residuals, flow fields, and scalar fields.

Frontal area considerations

The reference area in cycling is the projected frontal area. In this study, the frontal area of the cyclist was measured using an orthographic rendering of the 3D model (Figure 3) to represent the effective "shadow" of the body projected at an infinite distance. The frontal area in the standard position, with 175 mm crank lengths, was 0.444 m². This value decreased to 0.437 m² (a reduction of 1.6%) when the position of the trunk was rotated downward due to the shorter 165 mm crank length.
The reduction in frontal area with the 165 mm crank length setup, a decrease of 70 m², is primarily due to the head overlapping the torso silhouette and, more significantly, the trunk's increased horizontal inclination. The difference between the postures in the frontal area of the two legs is irrelevant.

Frontal area measures for the two postures — Figure 3: Frontal area of the two positions. Their percentage difference is 1.6%.

Normal area

The frontal area measurements focus on the area of the body directly impacted by the frontal flux of air. In a broader approach, the entire exposed area—even if behind parts of the body—could be considered (red color in Figure 4). To account for this surface, the normal area relative to the wind direction x of the cyclist's body was calculated. The results showed a value of 0.473 ² for the cyclist with the 175 mm crank length and 0.470 ² for the cyclist with the 165 mm crank length, reflecting a reduction of 0.6%. While both values are higher than the frontal area values, as expected, this is due to the inclusion of hidden areas—such as the abdomen behind the hands, the upper chest , and the back of the neck and middle shoulder—in the helmet's shadow (Figure 4). These areas are excluded when calculating the frontal area, as demonstrated in the following animation.

View of the surface normals directions — Figure 4: Body surface colored by the orientation of the outward-facing unit normal vectors. Red is the orientation towards the flow direction and blue opposite to it.

Differences of the surface normals directions

This animation of the top views for both positions highlights how the back area, pointing toward the fluid direction (red), increases in the 165 mm crank length position due to torso rotation. This increase in the frontal area of the shoulders and back for the 165 mm crank posture is counterbalanced by a greater reduction in the thorax and abdomen due to the tuck position.

Results of the CFD simulation

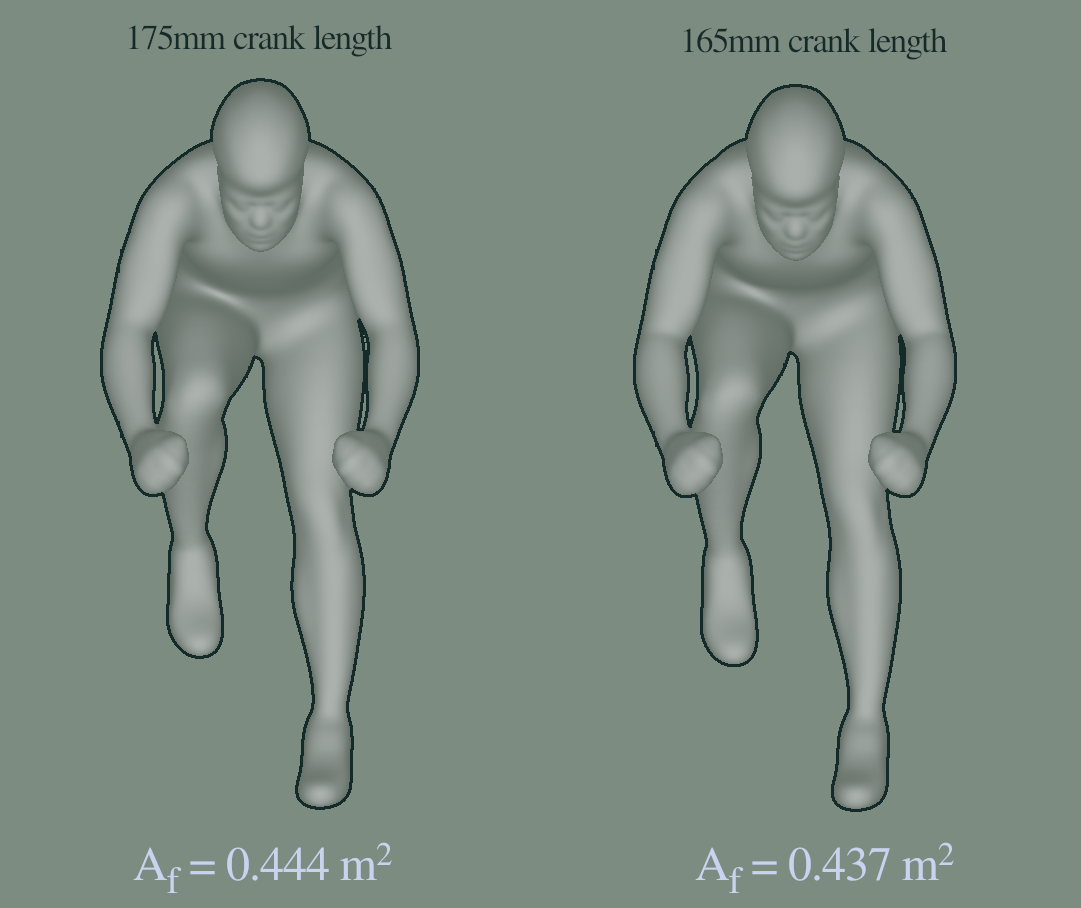
The sum of the pressure force (28.61 N) and the viscous force (1.07 N) causes the cyclist using the 175 mm crank length to experience a total force of 29.67 N. As shown in Table 1, the posture with the 165 mm crank length results in a total force of 28.70 N, representing a reduction of 3.38%. This force consists of a pressure force of 27.67 N (a decrease of 3.40%) and a viscous force of 1.03 N (a reduction of 2.91%). The overall lower drag for the 165 mm crank arm posture is attributed to a combination of a lower frontal area (-1.60%) and a lower drag coefficient (-1.64%).

Table 1: CFD results, blue for the position with the 175 mm crank length and red for the 165 mm.

	175 mm crank length	165 mm crank length (compared to 175 mm crank length)
Total drag force	29.67 N	28.70 N (-3.38%)
Pressure force	28.61 N	27.67 N (-3.40%)
Viscous force	1.06 N	1.03 N (-2.91%)

Frontal area	0.444 m²	0.437 m² (-1.60%)
C_d (frontal area)	0.556	0.547 (-1.64%)

Normal area	0.473 m²	0.470 m² (-0.64%)
C_d (normal area)	0.522	0.508 (-2.75%)

To explain the lower drag coefficient, an indicator of the bluffness of an aerodynamic body, the primary aspect to analyze is the airflow behavior over the back in both positions. The fluid over the red areas of the shoulders and the spine exhibits elevated velocity, indicating a flow attached to the surface of the body (Figure 5a and Figure 6a). When the color changes abruptly to light, it signals the absence of velocity near the body, likely caused by flow separation. Light blue zones in the plot—representing the x-component of velocity—indicate reverse flow due to vortices.
The following wall shear stress plots (Figure 5b and Figure 6b) help to further understand the flow behavior. On the back, regions where the color shifts to dark blue indicate very low shear forces (close to 0), indicating that the flow is no longer attached to the body. This marks the position of the separation point.
Comparing the plots on the left (Figure 5) with the corresponding plots on the right (Figure 6) reveals that the 165 mm crank length posture maintains a longer airflow attachment to the back, resulting in reduced drag.

Figure 5: Posture with the 175mm crank length. (a) Plot of the fluid velocity near the body. (b) Wall shear stress plot.

Figure 6: Posture with the 165mm crank length. (a) Plot of the fluid velocity near the body. (b) Wall shear stress plot.

The sagittal section plots (Figure 7 and Figure 8) show that, for the 165 mm crank length posture, the velocities on the cyclist’s back are higher, indicating a favorable condition.
The plots also reveal that the helmet used by the cyclist has design limitations, as a minor change in head inclination causes a major change in the wake generated by the helmet. The 165 mm crank condition, which results in a more horizontally inclined head position, generates a larger wake with an upward inclination. These conditions lead to higher drag for the cyclist, despite being in the most aerodynamic posture.

Figure 7: 175 mm crank length, side section view. (Top) Magnitude velocity color-coded plot. (Bottom) Line Integral Convolution (LIC), color-coded by velocity magnitude.

Figure 8: Posture with the 165mm crank length, side section view. (Top) Magnitude velocity color-coded plot. (Bottom) Line Integral Convolution (LIC), color-coded by velocity magnitude.

Final remarks

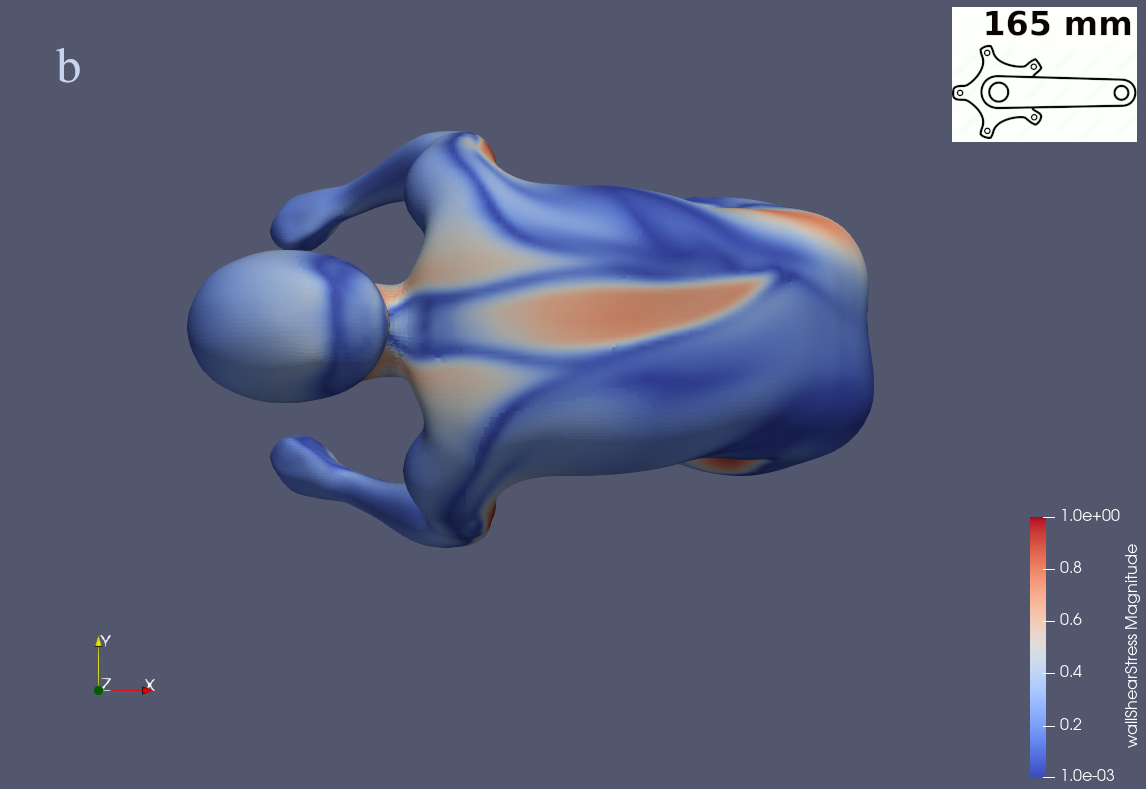
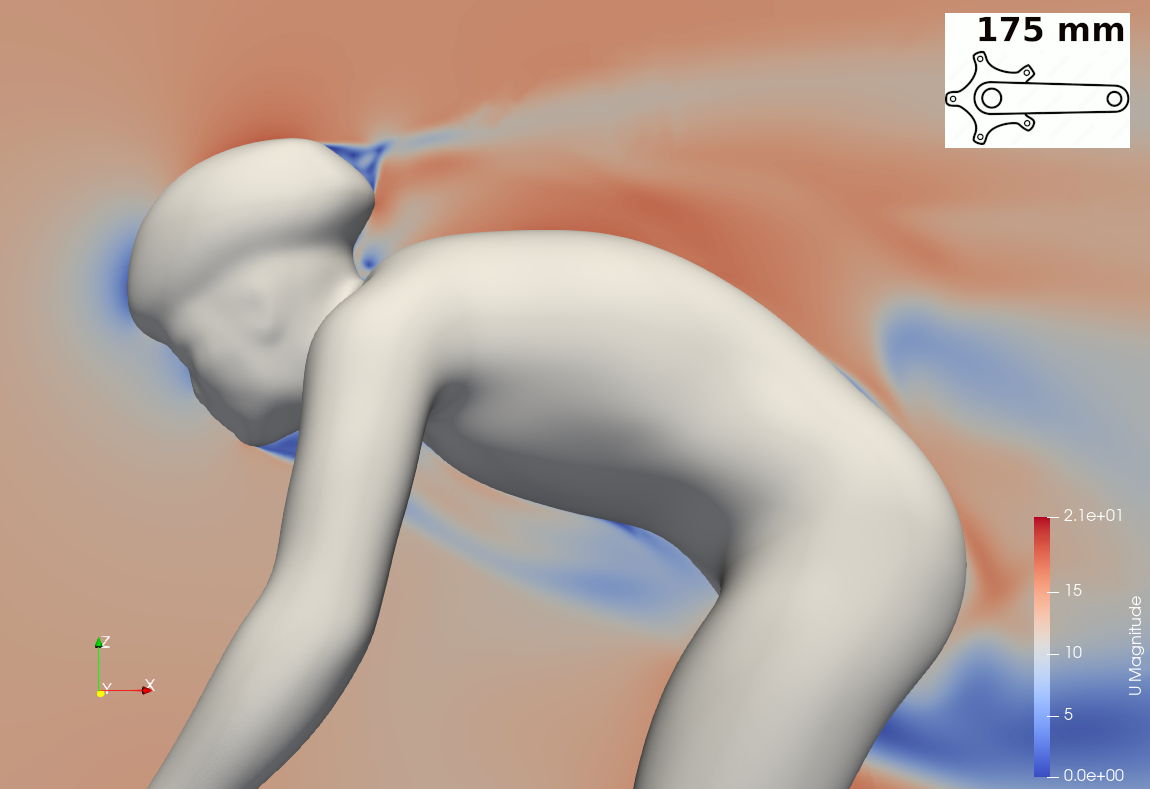
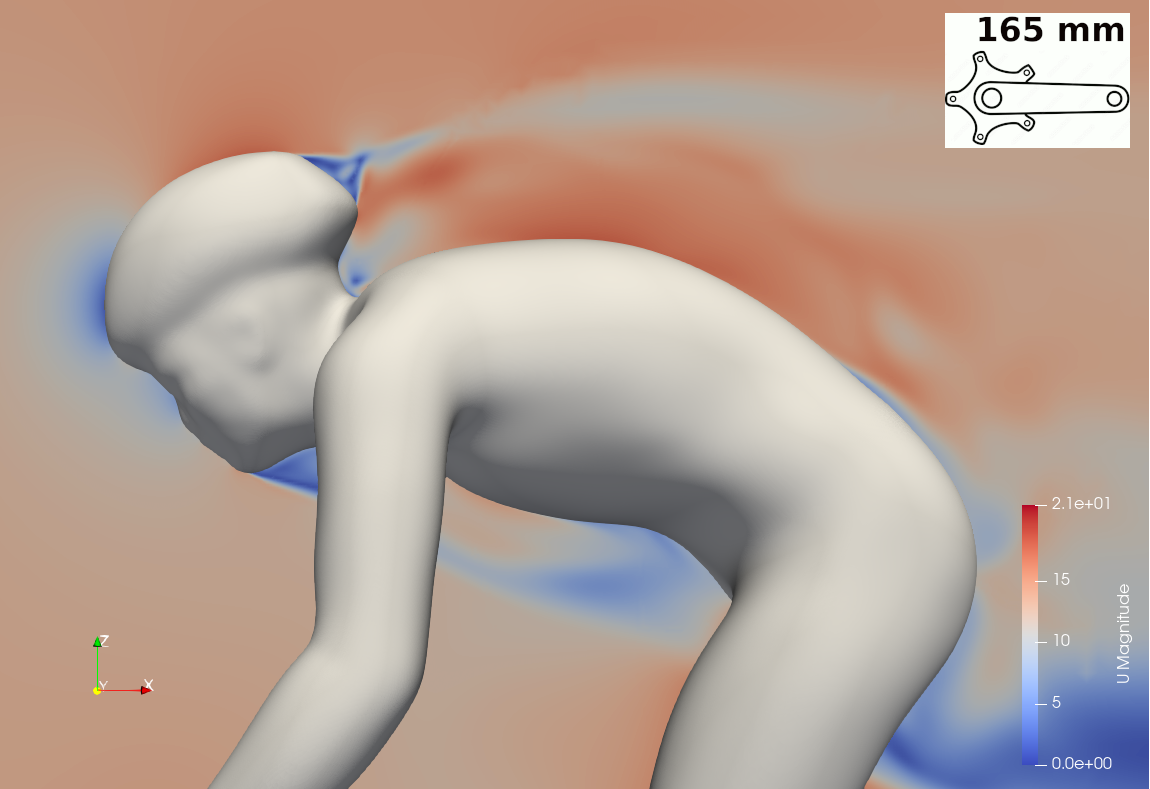
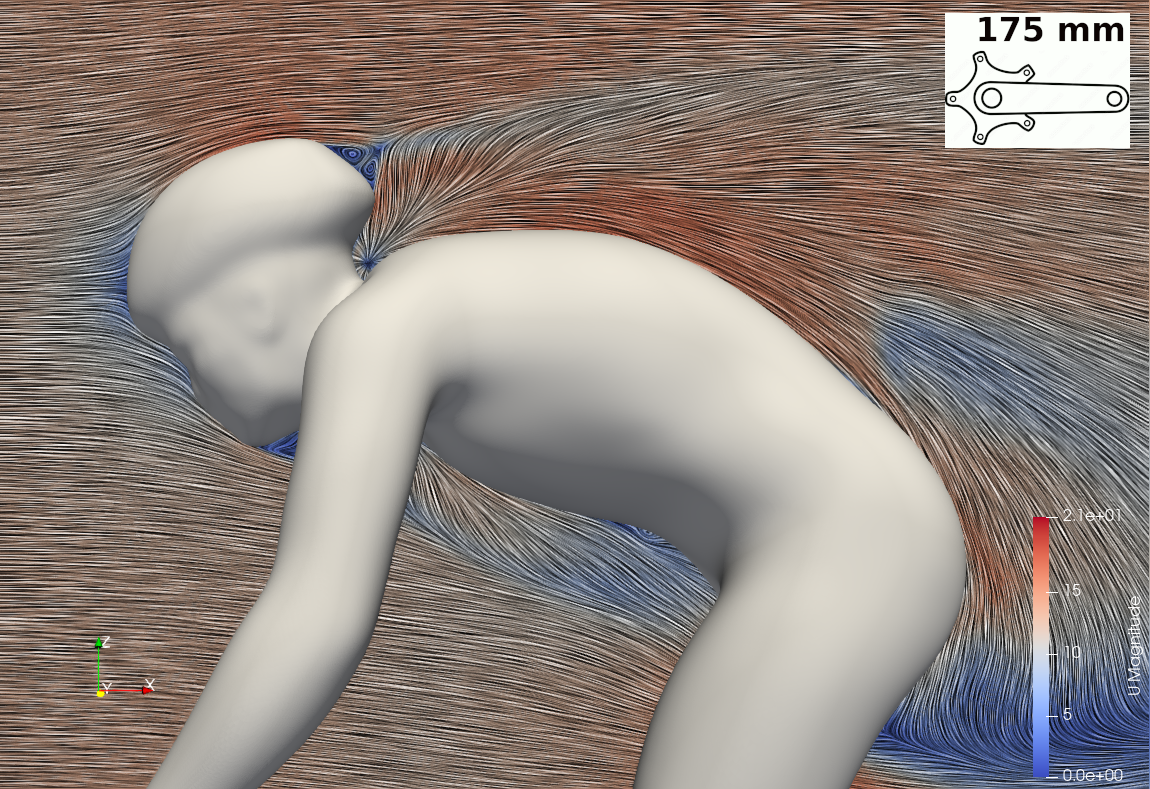
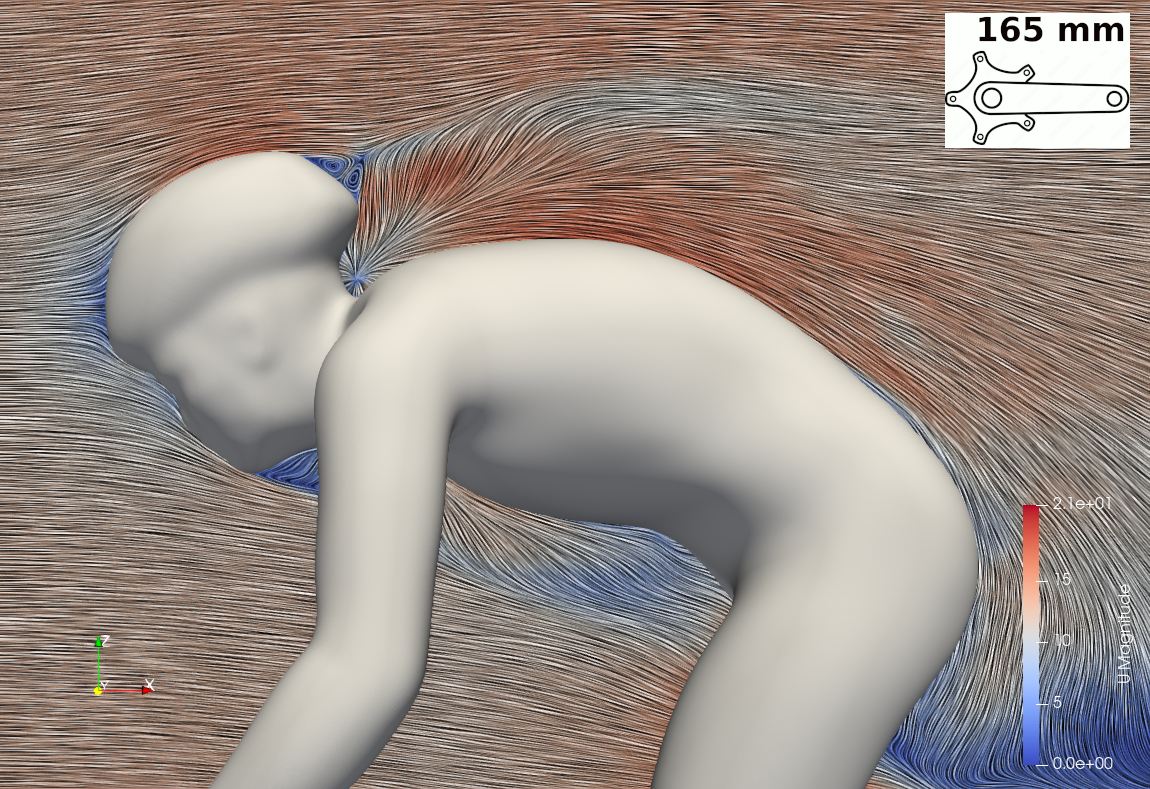
In this study, CFD simulations show that a shorter crank length combined with a lower torso position is an effective combination for reducing drag force. The posture identified as the “165 mm crank length posture” resulted in a significant 3.38% reduction in drag compared to “175 mm crank length posture”, and this value could be further improved with a properly designed helmet. Two approaches for determining the reference area were employed: the frontal area and the “normal area.” The contribution to the drag force is attributed to both a lower drag coefficient (C_d) and a smaller reference area. Depending on the reference area approach, their influence varies: the two factors have nearly identical effects when the frontal area is used, while the drag coefficient plays a much more significant role when the normal area approach is applied.

Reduced drag with a shorter crank arm

Decreased drag with shorter crank length